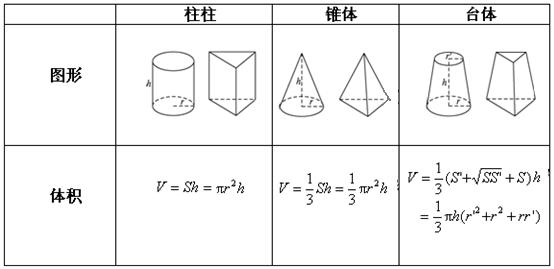
三角 錐 体積 公式
四角錐台の体積を計算する必要がありました。上記公式に数字を当てはめるとA=43 B=36 a=29 b=19 h=18 単位cmです。公式に当てはめて計算してみると大方18リットル=10升=?斗であることがわかりました。.

三角 錐 体積 公式. 三角錐の体積の求め方についてです! 三角錐に内接する球の半径×表面積÷3と出てきたのですが、これは公式ですか??また、なぜこのような式が成り立つのですか?? usameros0501sさん三角錐の4つの面積をa,b,c,dとし、球の半径をrとすれば、三角錐は、底面積がそれぞれa,b,c,dで高さがrの三角錐4. この記事では「三角錐」についての公式(体積・表面積)や実際の求め方をできるだけわかりやすく解説していきます。 この記事を通してぜひマスターしてくださいね! 目次三角錐とは?三角錐の体積の公式三角錐の体積の求め方三角錐. エレガント三角 錐 表面積 公式 圓錐體的表面積六年級數學 Grade 6 Math Surface Area Of A Cone.
簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事. 三角錐の体積=底面積×高さ× 1 3 証明. このとき、三角錐 O-ABC の体積Vは、次式で与えられる。 (証明1) 3点A(a 1 ,a 2 ,a 3 )、B(b 1 ,b 2 ,b 3 )、C(c 1 ,c 2 ,c 3 )を通る平面の方程式を ax+by+cz=1 とすると、原点Oから平面への距離 h は、.
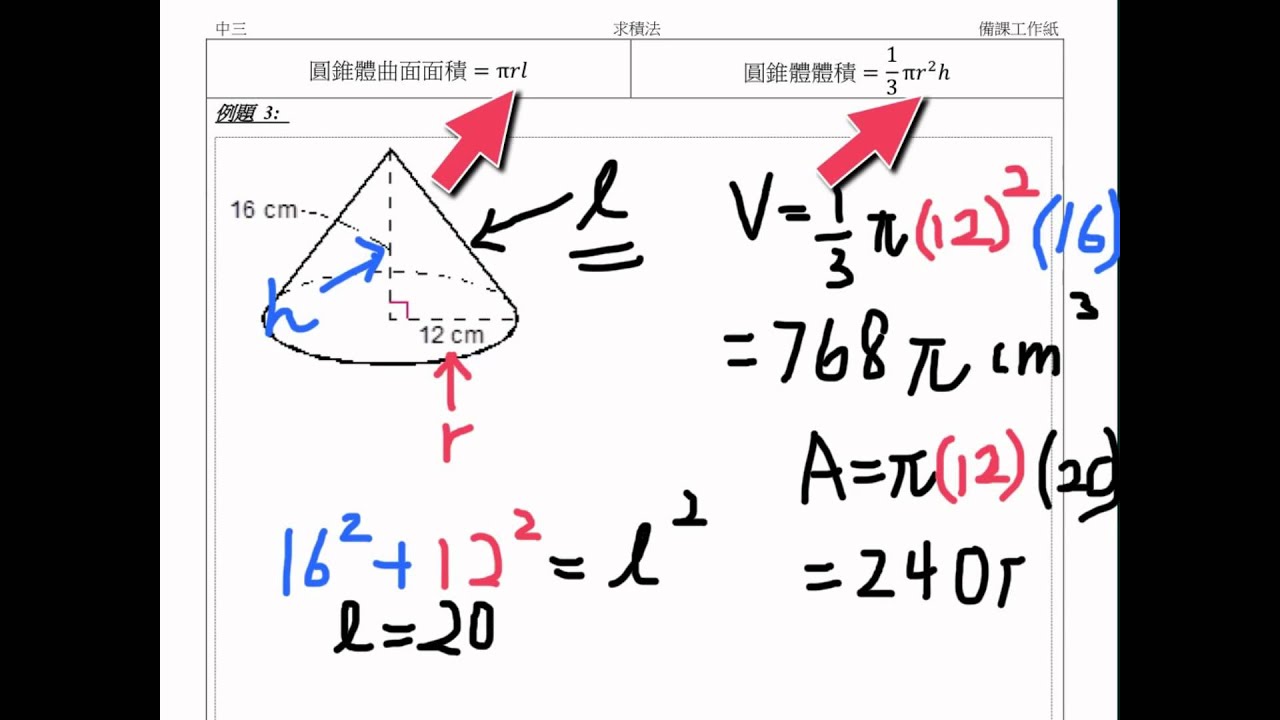
この公式は、これまでに説明してきた求め方にしたがうことで簡単に導くことができます。 (底面の円の面積)=(半径)×(半径)×(円周率)=r × r × π= πr 2 (円柱の体積)=(底面の円の面積)×(高さ)=πr 2 ×h= πr 2 h. 松谷です。 先日、小学生に、三角錐とか四角錐とか円錐の体積について、教えていて、 何やら1/3という数字に納得が行かなそうな顔をしていた ので、少し追加で話してみました。. またまた「小中学生にもわかる」シリーズだが、 今回は「錐体の体積は底面積×高さ÷3」 という公式についてである。 この公式は小学校高学年で教わることになっているが、 子供に 「なんで÷3かわかる?」 と聞くと、.
角錐・円錐の体積と表面積の公式 管理人 2月 5, 19 / 2月 15, 19 主に柱体(角柱・円柱)、錐体(角錐・円錐)、球の3種類の立体です。. シンプソンの公式は単純な積分のみならず、考え方次第では体積を求めるのにも使えます。 今回はその例をいくつか紹介します。 Ⅰ 体積への拡張 Ⅱ 三角柱の体積 Ⅲ 円錐の体積 Ⅳ 四角錐台の体積 Ⅰ 体. 体積 (たいせき) とは、 立体 (りったい) が 空間 (くうかん) の中で 占 (し) める大きさのことです。.
V = 体積 A = 球体の表面積 r = 球体半径. 頂点bを含む三角錐、頂点dを含む三角錐、頂点eを含む三角錐、頂点gを含む三角錐の4つある。 eを含む三角錐で体積を出してみる。 eh=ef=6なので efhの面積は6×6÷2=18 efhを底面とするとae=6が高さとなるので 体積は 18×6÷3=36. 初歩的な質問ですが、 円錐や三角錐の体積を求める公式が 底面積×高さ×1/3 というのは知っています。 ただ公式として3分の1にするのは知っているのですが、なぜ3分の1にするのかを数学的知識が乏しい(中学校1年生など)にうまく説明する方法はない.
一組得れば、事足れり。あとは、底面の三角形を、相似拡大と 三角形の等積変形で目的の三角形に変換すればよい。 三角錐と三角柱の両方に同じ変換を施しておきます。 高さ方向にも拡大した後、錐の頂点を底面に平行にずらせば完了。. むちゃ便利だけど、 なんで公式で計算できちゃうんだろう?? ちょっと怪しい笑. V = 体積 S = 角錐底面積.
3 円錐と三角錐の体積に関する公式が同一であること 4 底辺が正方形で、側面が全て正三角形の四角錐 底面積が72平方センチメートル この時の体積を求めなさい 5 中2?の図形のところです。数学です。 この問題は、6つの三角錐の体積を引く以外に体積は求め. 下の図の三角錐で, 三角錐a-dpeと三角錐a-bqcの体積比は になる。 証明. 「三角錐の体積・表面積がわからん!」 「とにかく求め方をサクッと知りたい!」 という方に向けて、今回の記事では三角錐の計算について3分で理解できるようにまとめています。 この記事を読みながら手元の宿題やワークを一緒に解き進めていき.
計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学び. 三角錐の内接球を求めるには、 三角錐の体積と表面積から方程式を立てるのが有効 ということでした。 実はこの考え方は三角錐によらず、あらゆる多面体に対して使うことができます。. 証明 abcを底面として三角錐を考えると, 公式より底面の面積比は である。 ここでその底面に対する高さは, 上の図から, ah p∽ ah qを使って, よって,.
要点…四角錐,三角錐,円錐の体積 三角錐,四角錐,円錐の体積 V は,それがちょうど入る四角柱,三角柱,円柱の体積の です. 特に,円錐については,底面の半径が r であるとき,底面積が S=πr 2 と書けるから と書くこともできます.. 錐体の体積が3分の1になる理由? Category - 数学, 松谷, 独り言 松谷 コメント(0). V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積.
このページでは、 様々 (さまざま) な立体の体積の 求 (もと) め方を 一覧 (いちらん) にまとめています。 図形 (ずけい) と体積の 公式 (こうしき) をセットで 覚 (おぼ) えましょう!. よって、三角錐の体積は、 $\dfrac{1}{3}$× (底面積) × (高さ) $=\dfrac{1}{3}\times$ $3$ $\times$ $4$ $=4\:\mathrm{cm^3}$ となります。 この問題は高さがすぐに求まりましたが、高さを頑張って計算しないといけない問題もあります。 関連:正四面体の高さと体積の求め方. 角錐 pyramid V = 体積 S = 角錐底面積.
柱體和錐體 23 直圓錐的表面積計算 Youtube. 今回は、三角柱の体積の求め方公式について書いていきたいと思います。 // 三角柱の体積の求め方公式 三角柱の体積を求める問題 問題① 《三角柱の体積の求め方》 問題② 《三角柱の体積の求め方》 問題③ 《三角柱の高さの求め方》 問題④ 《三角柱の高さの求め方》 三角柱の体積. 正三角錐の底面には正三角形があります。 この三角形の高さは、その辺の長さに等しいことが関係しています。 h 0 = √3 / 2 * a。 この式を前の段落に書かれている三角錐の体積の公式に代入すると、次のようになります。.
V = 体積 A = 円錐面積 r = d/2 = 半径. Http Www Chwa Com Tw His Zipup Mathpublication Math 002 1010 Pdf 求める四角錐の高さcmとなります 答え 9cm 立体の体積表面積を求める公式. まとめ:三角錐の体積の求め方の公式は3ステップ! 三角錐の体積の求め方をマスターしたね。 ようは、 底面積をだして、 高さをかけて、 最後に「3」でわればいいんだ。 問題をときまくって公式になれていこう! そんじゃねー.
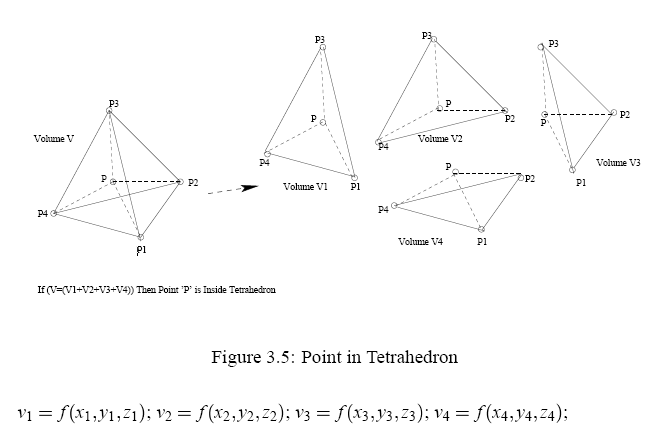
三角柱を3つの三角錐に分解することで証明する. (Ⅰ)三角錐 と三角錐 について 三角柱 の側面 は平行四辺形である.. 今日はそんな流れで、 台形の体積(正四角錐)の求め方をみちびいてみよう! 3ステップでできちゃうよ。 Step1. 多面体の体積(三角錐) 「ここからは、多面体の体積を考えるとしよう。 まずは、簡単なところで、下図のような三角錐の体積を求める。 ここで、点hは、必ずしも、三角形p1-p2-p3の面内にあるとは限らんが、底面に対してaから引いた垂線の足じゃ」.
三角柱を3つの三角錐に分解することで証明する. (Ⅰ)三角錐 e-afc と三角錐 e-afd について 三角柱 abc-def の側面 acfd は平行四辺形である..

Asp 討論版

Asc Mathsecrets 題目 Asc 求積法 如果對呢個topic 唔熟既話 可以 Facebook

体积公式图解 第1页 要无忧健康图库
三角 錐 体積 公式 のギャラリー

三角锥体积公式 第1页 一起扣扣网

正四面體regular Tetrahedron 的高和邊長的關係 學校沒有教的數學

三角锥体积公式 第1页 一起扣扣网

梯形体计算 梯台体的体积计算公式梯体的体积计算公式是什么 尚书坊

圆柱体积公式 圆柱体积公式画法
Q Tbn 3aand9gcsctjffpzud2veknyzeuwvuykto64pbcf0ufrahaelkpjiwkdfy Usqp Cau

圆锥与球与圆柱

中1数学 三角すい 四角すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット

幾何 國小數學教材分析
数理天地

柱體和錐體 23 直圓錐的表面積計算 Youtube

三角锥体积公式图解 第1页 要无忧健康图库

Frustum的體積公式 Kotze223
Www Takwing Idv Hk Dse Room Dse Maths Teaching Junior Junior 14 Area N Vol 4 Pdf

計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
三度空間的插值法

體積的重心求法

三角锥体积公式图解 第1页 一起扣扣网

圆锥的表面积公式 圆锥的表面积公式画法
Q Tbn 3aand9gcrdmbjf023snhchunm8igshytquotzyqmhz0d1izjj7pjdycadg Usqp Cau

簡単公式 三角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

柱體和錐體 23 直圓錐的表面積計算 Youtube

梯形体体积计算公式与在线计算器 三贝计算网 23bei Com
Q Tbn 3aand9gctvangbvg5qupnaajbnzskxn0wqondvlsdlvmmah1e Usqp Cau
圓錐 分類 定義 組成 測量 高 底面周長 表面積 體積 繪製方法 展開圖 三視圖 中文百科全書

三角锥体积公式 第1页 一起扣扣网

正四面體regular Tetrahedron 的高和邊長的關係 學校沒有教的數學

圆的体积公式图片大全 Uc今日头条新闻网

四面體 維基百科 自由的百科全書

圓錐表面積的算法 耕圃莘園 隨意窩xuite日誌

三角形怎么计算立方 你搜我答

方体的体积公式 圆柱体体积公式 四棱台体积公式 圆锥体的体积公式 Www Dingjisc Com

三角锥形体积公式 第1页 一起扣扣网

錐體體積 1 3柱體體積的3種證明法 Ishewh的創作 巴哈姆特

四角锥体积 4棱锥体积公式 四棱锥面积公式 V棱锥的公式

圆锥体的体积公式是怎么推导出来的 知乎

錐體體積 1 3柱體體積的3種證明法 Ishewh的創作 巴哈姆特
錐體體積 1 3柱體體積的3種證明法 Ishewh的創作 巴哈姆特

三角体的体积公式 第1页 一起扣扣网

三角锥体积公式图 第1页 一起扣扣网

三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学

高中數學每日一題3 31 每日頭條

截头方锥体体积 表面积 周长 质量 对角线在线计算器 三贝计算网 23bei Com

稜錐 維基百科 自由的百科全書

三角棱锥体 Www Shianwang Com
Q Tbn 3aand9gcs28eh Aeh6 Enoh7qwgcaxcvwnppqmemqocpxyhnjvihoroiaz Usqp Cau

圆台表面积与体积公式 学习岛
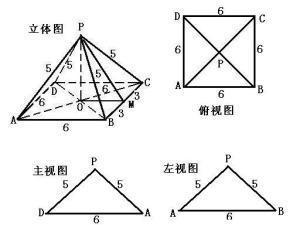
正四棱锥体积和表面积的计算公式 是什么 360问答
数理天地

三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学

飞时达三角网法计算土方原理 公式 小傅博客

截头圆锥的体积计算怎么算截头圆锥的表面积啊

四面體 維基百科 自由的百科全書

梯形体公式 梯形的体积公式是什么是梯形体梯形体的体积公式是什么 尚书坊

簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ

非常有用的常用求面積 體積公式 非常有用收藏吧 每日頭條

體積公式 體積公式 即計算各種幾何體體積的數學算式 比如 圓柱 稜柱 錐 百科知識中文網
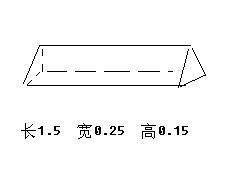
三角体体积计算公式 360问答

角錐體積公式的由來 Youtube

3分でなるほど 三角錐の体積 表面積の求め方をマスターしよう 数スタ

方锥台体积公式及图解 第1页 一起扣扣网

四面體 維基百科 自由的百科全書

柱體的體積與表面積 06 底面是直角三角形的三角柱的體積求法 Youtube

錐台 Wikiwand

数理天地

截头圆锥体体积 表面积 质量计算公式与在线计算器 三贝计算网 23bei Com

三角形体积计算公式 三角体体积公式 圆柱体积公式 三角形的表面积

三角锥体积公式图 第1页 一起扣扣网

正四面积体体积 表面积计算公式与在线计算器 三贝计算网 23bei Com

直角锥体积 表面积 侧面积 计重 报价计算公式与在线计算器 三贝计算网 23bei Com
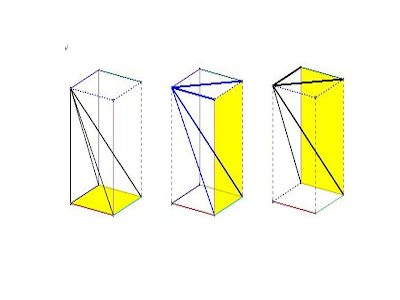
快樂ˇ有趣的理化課 八月08

角錐 円錐の体積と表面積の公式 数学fun
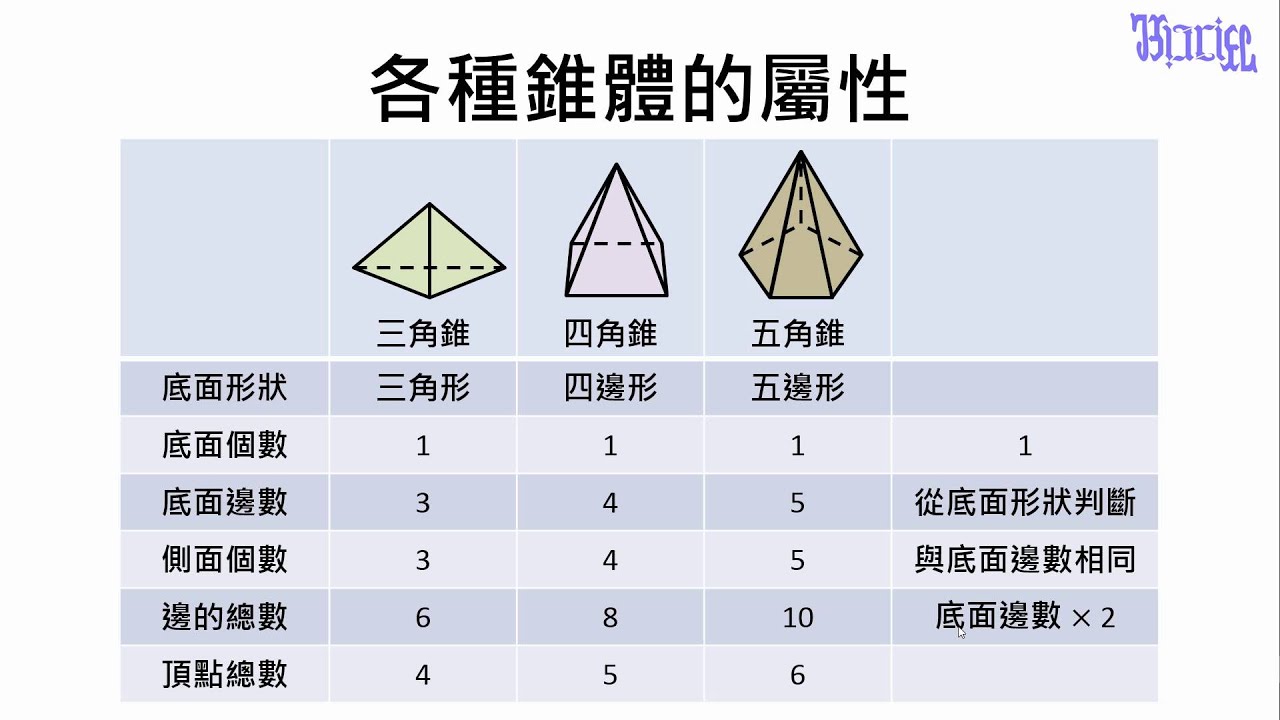
柱體和錐體 18 錐體的共通屬性推導 Youtube

三角锥形体积 三角形体积计算公式 三角锥的体积公式 三角柱体积公式
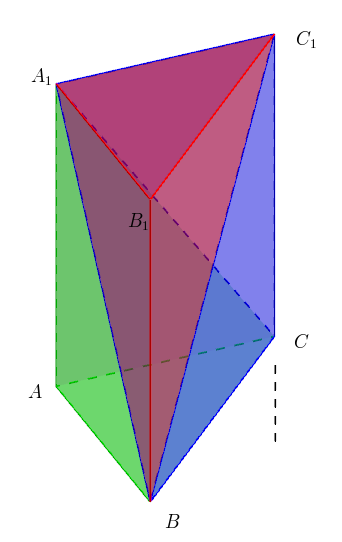
柱 锥 台 球的体积公式推导 不用积分 Li Hua 博客园

高中數學必修二立體幾何突破點 二 空間幾何體的表面積與體積 每日頭條
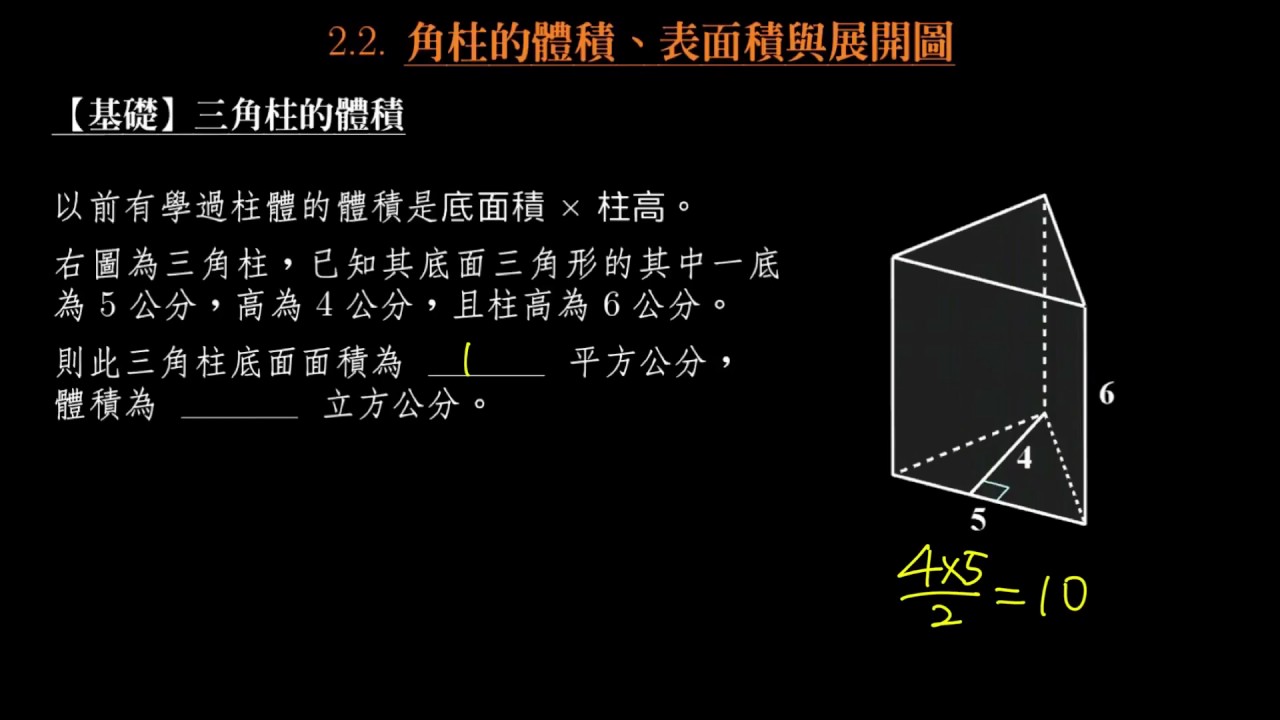
基礎 三角柱的體積 Youtube

7 稜柱 稜錐 稜台和圓柱 圓錐 圓台的體積 球的表面積與體積 每日頭條
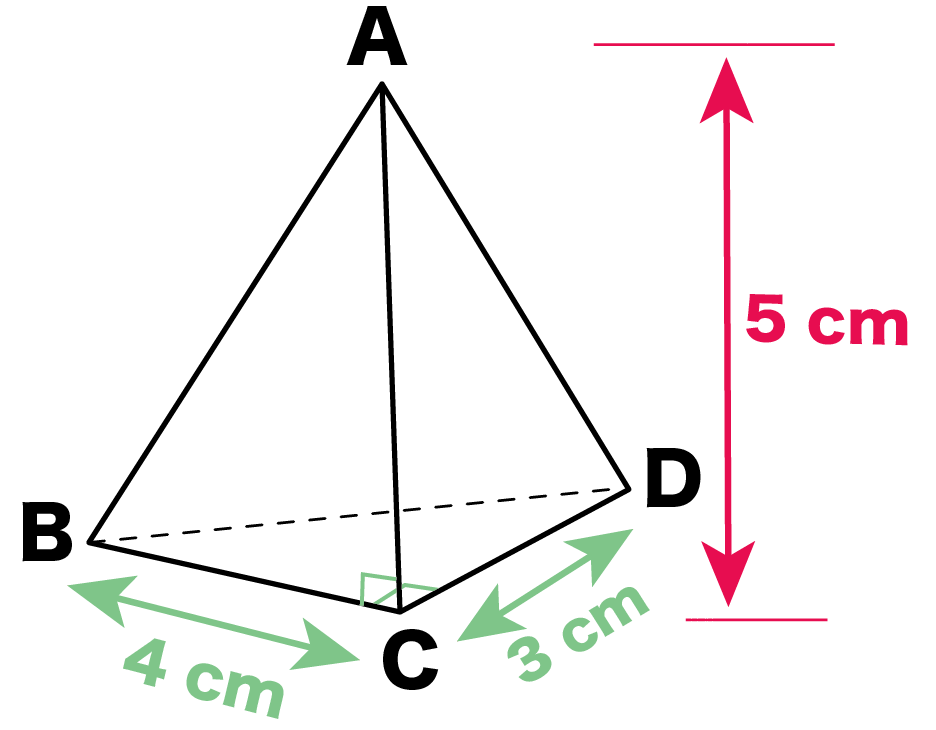
三角形高公式 三角形的高公式 三角形高怎么算 求三角形的高

圓錐體的表面積六年級數學 Grade 6 Math Surface Area Of A Cone Youtube

簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ

例題短解 7 Area And Volume 面積及體積 Youtube

高考 立体几何 圆台体积公式推导 设公比法最简单 哔哩哔哩 つロ干杯 Bilibili

7 稜柱 稜錐 稜台和圓柱 圓錐 圓台的體積 球的表面積與體積 每日頭條

鈄截柱體體積 Quod Erat Demonstrandum
錐體體積 Youtube

圓錐體積公式 圓錐體積公式 快熱資訊 走進時代

圓錐 圓錐 數學領域術語 有兩種定義 解析幾何定義 圓錐面和一個截它的平面 滿足交線 華人百科

锥形体积 圆锥形体积 三角锥形体积 棱锥表面积

三角柱体体积 第1页 一起扣扣网

錐體體積 1 3柱體體積的3種證明法 Ishewh的創作 巴哈姆特
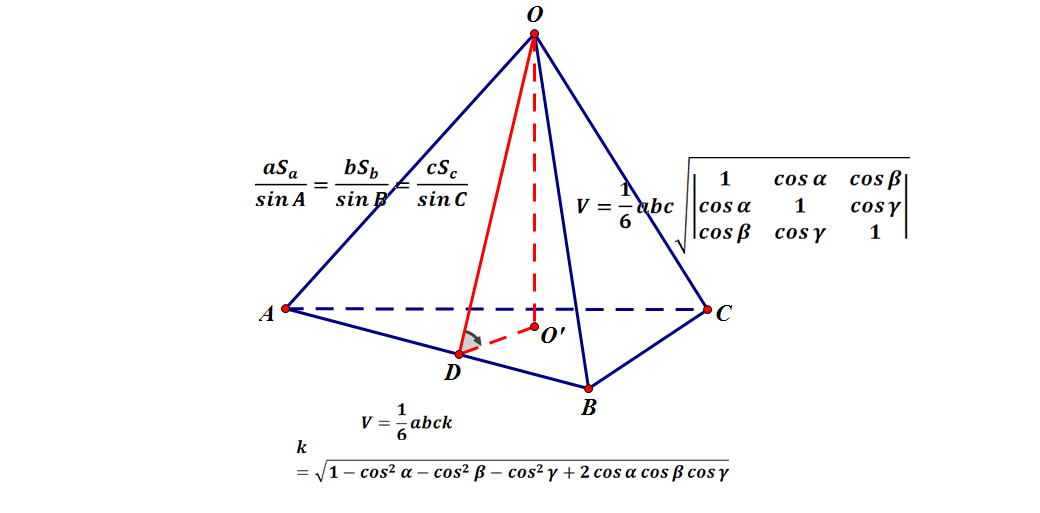
四面体体积公式 知乎
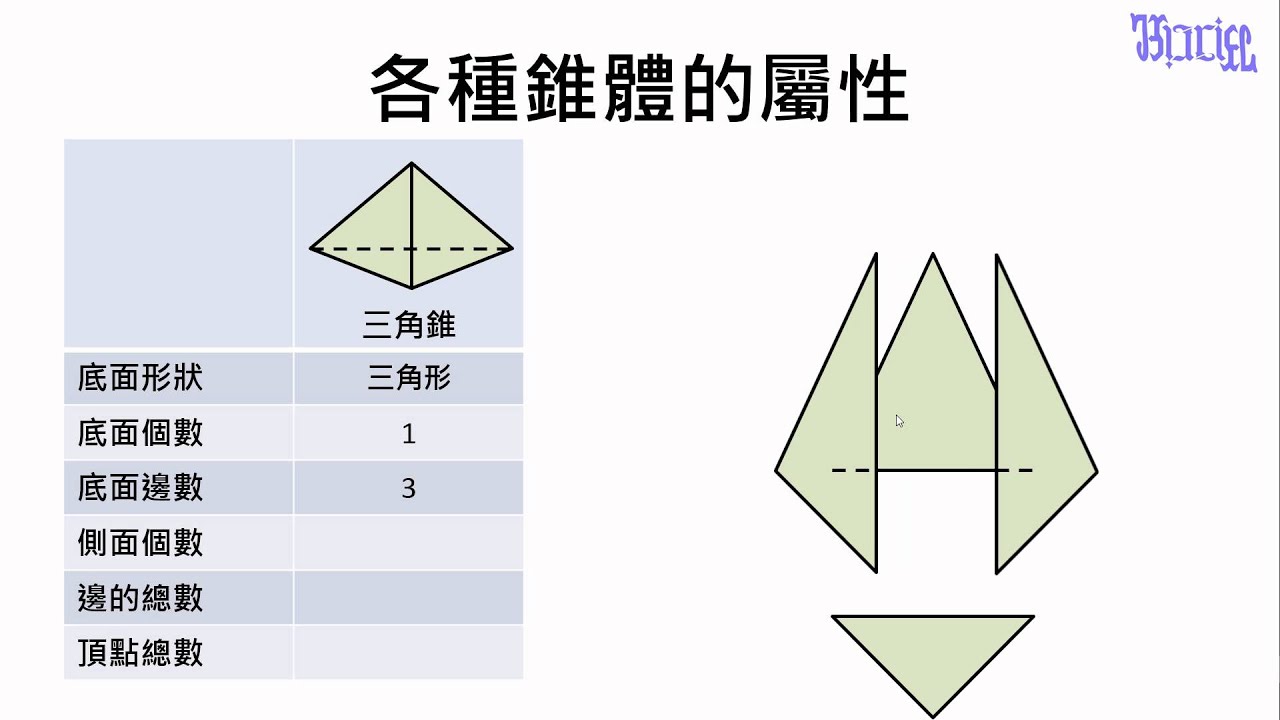
柱體和錐體 15 三角錐的屬性 Youtube
圓台 維基百科 自由的百科全書

高中數學立體幾何 由三視圖求錐體體積高效破解策略 終極結論一 每日頭條

正四面體regular Tetrahedron 的高和邊長的關係 學校沒有教的數學
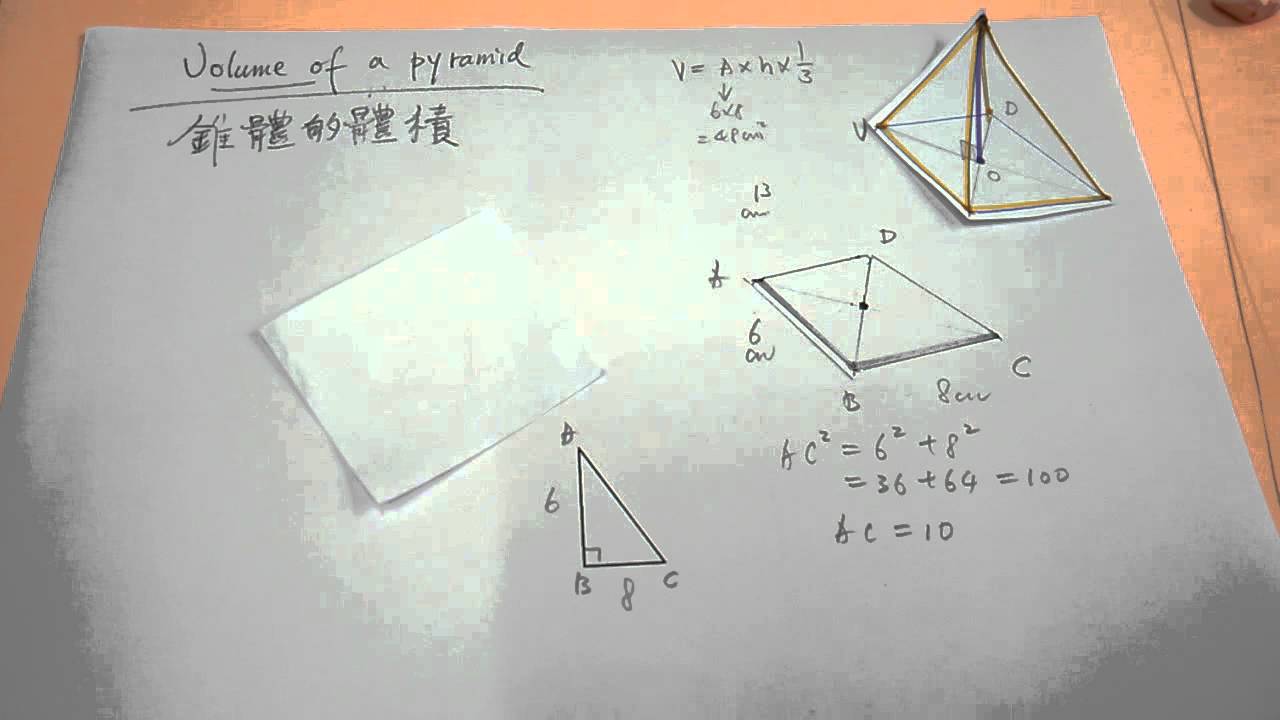
錐體體積 Youtube

圆锥体积公式推导图 圆锥体体积公式推导 尚书坊
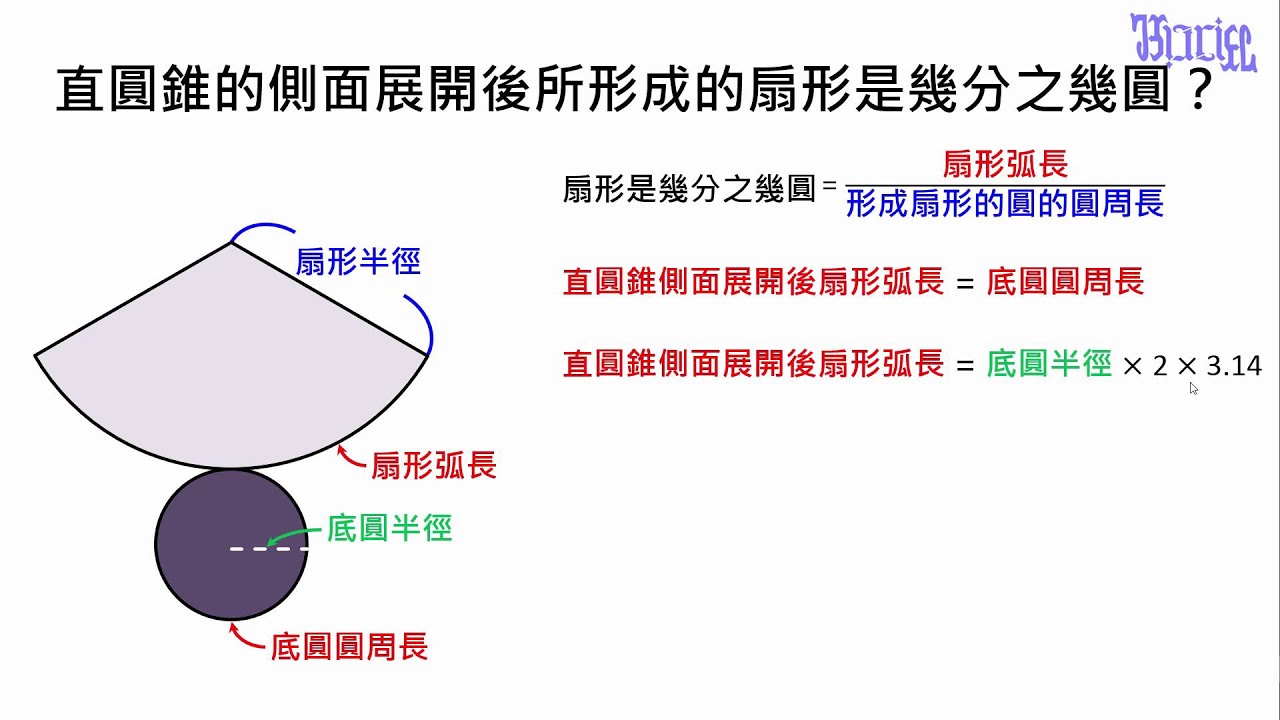
柱體和錐體 21 直圓錐側面扇形展開後是幾分之幾圓 Youtube

求四角梯形锥体积计算公式就是四面斜 上下两面是大小不一样的长方形 应该是台体吧 如果不是台体 求计算公式 作业 慧海网
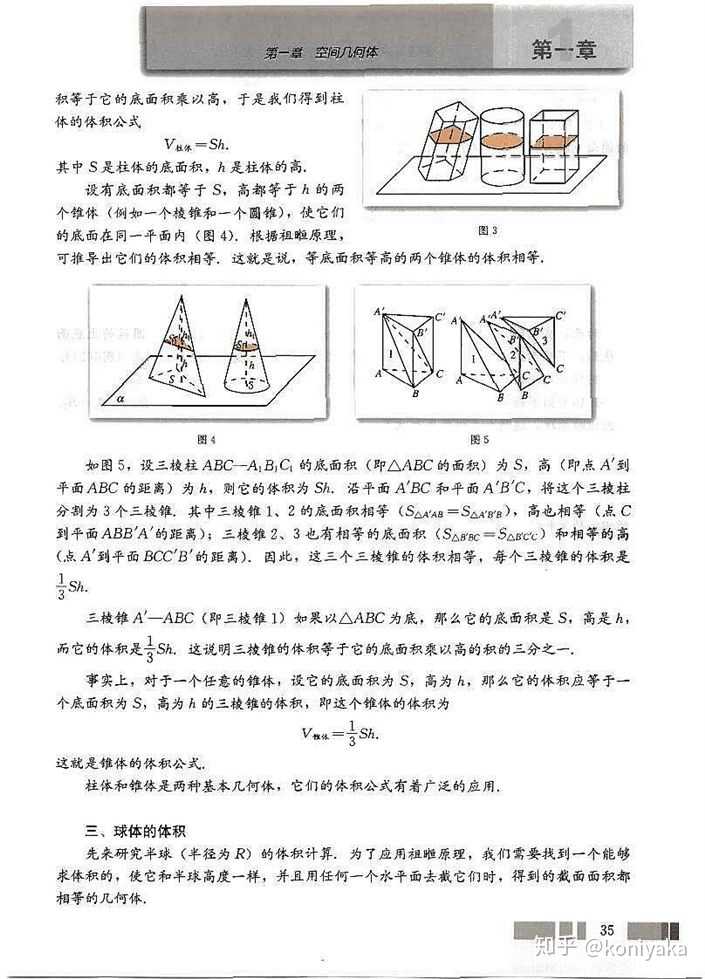
圆锥体的体积公式是怎么推导出来的 知乎




